

The first of the previous vector identities is also known as the problem of Sylvester.
EFINE ALTITUDE GEOMETRY FREE
From this, the following characterizations of the orthocenter by means of free vectors can be established straightforwardly: Is represented by the point, namely the orthocenter of triangle. In the complex plane, let the points, and represent the numbers, and respectively and assume that the circumcenter of triangle is located at the origin of the plane. Since barycentric coordinates are all positive for a point in a triangle's interior but at least one is negative for a point in the exterior, and two of the barycentric coordinates are zero for a vertex point, the barycentric coordinates given for the orthocenter show that the orthocenter is in an acute triangle's interior, on the right-angled vertex of a right triangle, and exterior to an obtuse triangle.
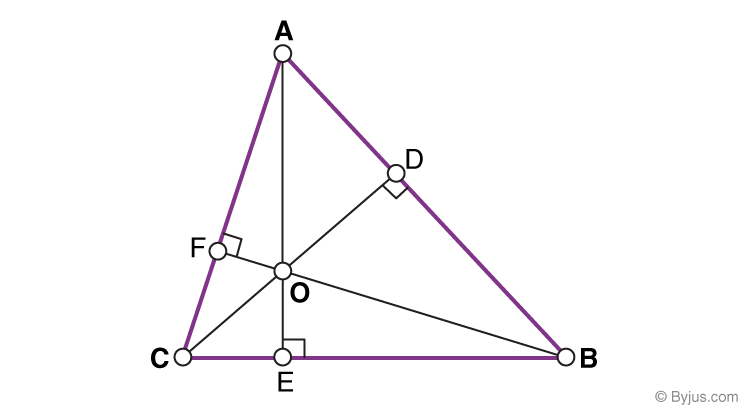
The orthocenter has trilinear coordinates Let A, B, C denote the angles of the reference triangle, and let a = | BC|, b = | CA|, c = | AB| be the sidelengths. The isogonal conjugate and also the complement of the orthocenter is the circumcenter.įour points in the plane such that one of them is the orthocenter of the triangle formed by the other three are called an orthocentric system or orthocentric quadrangle. In terms of the sides a, b, c, inradius r and circumradius R, :p. The orthocenter is closer to the incenter I than it is to the centroid, and the orthocenter is farther than the incenter is from the centroid:
The center of the nine-point circle lies at the midpoint between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half that between the centroid and the orthocenter: The orthocenter H, the centroid G, the circumcenter O, and the center N of the nine-point circle all lie on a single line, known as the Euler line. 176 This product is the squared radius of the triangle's polar circle. The product of the distances from the orthocenter to a vertex and to the foot of the corresponding altitude is the same for all three altitudes. If one angle is a right angle, the orthocenter coincides with the vertex of the right angle. does not have an angle greater than or equal to a right angle). The orthocenter lies inside the triangle if and only if the triangle is acute (i.e. The three (possibly extended) altitudes intersect in a single point, called the orthocenter of the triangle. The altitudes are also related to the sides of the triangle through the trigonometric functions. Thus the longest altitude is perpendicular to the shortest side of the triangle. It is a special case of orthogonal projection.Īltitudes can be used to compute the area of a triangle: one half of the product of an altitude's length and its base's length equals the triangle's area. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude of that vertex. The length of the altitude, often simply called the altitude, is the distance between the extended base and the vertex. The intersection between the extended base and the altitude is called the foot of the altitude. This line containing the opposite side is called the extended base of the altitude. forming a right angle with) a line containing the base (the opposite side of the triangle). In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e. Three altitudes intersecting at the orthocenter


 0 kommentar(er)
0 kommentar(er)
